Contoh Soal Kurva Lorenz – Kurva Lorenz merupakan metode penggambaran pemerataan kekayaan (pendapatan) di suatu negara ataupun daerah. Dimana fokus utama pada kurva Lorenz ini adalah seputar ada atau tidaknya ketimpangan penghasilan penduduk di area tersebut.
Saat proses pembelajaran terkait kurva Lorenz, kamu akan dihadapkan pada soal berisi data pendapatan penduduk yang telah dikelompokkan dalam rentang tertentu. Kemudian data atau informasi dalam soal harus sepenuhnya di analisa hingga mendapatkan hasil akhir berupa gambaran kondisi penghasilan masyarakat.
Pengerjaan soal kurva Lorenz sendiri tersedia dalam 2 (dua) pilihan cara, yakni cara manual serta cara otomatis. Bila menggunakan cara manual maka kamu akan memerlukan bantuan kalkulator. Sementara jika dikerjakan secara otomatis maka alat bantu yang diperlukan adalah aplikasi pengolahan data seperti Microsoft Excel.
Pada kesempatan kali ini, Kursiguru akan menjelaskan mengenai contoh soal kurva Lorenz beserta cara pengerjaan dan jawaban soalnya. Dimana penulis akan berfokus pada cara pengerjaan secara otomatis, namun tak perlu khawatir karena nantinya file excel contoh soal bisa langsung didownload.
Dasar Kurva Lorenz
Sebelum membahas mengenai contoh soalnya, akan sangat baik jika kamu memahami dasar materi kurva Lorenz. Dalam ilmu dasar kurva Lorenz, terdapat bebepara komponen penting seperti garis diagonal utama (kemerataan), koefisien Gini dan juga kurva Lorenz itu sendiri.
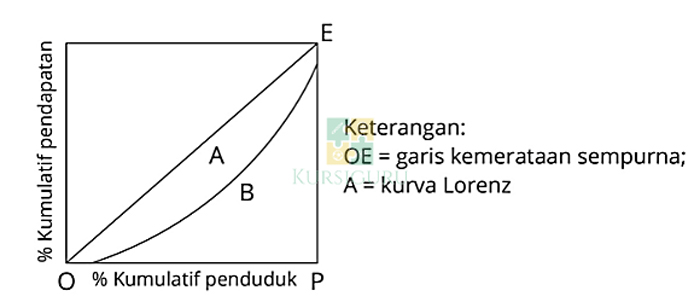
Melalui gambar di atas, seorang siswa bisa mengetahui beberapa informasi dasar kurva Lorenz yakni:
- Garis Diagonal Utama (OE) : kondisi ketika sebuah daerah memiliki kemerataan penghasilan secara sempurna.
- Kurva Lorenz : Lengkungan di bawah (OE).
- Koefisien Gini : Perbandingan antara luasan A & B.
Indeks Gini juga mampu memberikan penggambaran
Jenis Kurva Lorenz
Setelah mengetahui mengenai dasar pembelajaran kurva Lorenz, selanjutnya seorang siswa perlu tahu perihal jenis kurva Lorenz. Dimana berdasarkan kondisi hasilnya, kurva Lorenz terbagi menjadi 2 (dua) jenis yakni kurva Lorenz normal serta kurva Lorenz ekstrem.
Kurva Normal
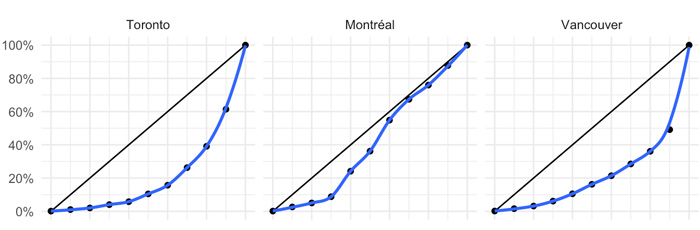
Kurva Lorenz normal adalah sebuah kurva yang memiliki perbandingan lengkungan kurva tidak terlalu jauh dari garis diagonal utama. Dengan kata lain, kurva normal mempunyai koefisien gini antara 0 hingga 1. Berikut ini adalah contoh kurva Lorenz normal.
Kurva Ekstrem
Sementara kurva Ekstrem merupakan sebuah kurva dengan perbandingan lengkungan sangat jauh di bawah (OE), memiliki kurva di bawah titik nol ataupun bentuknya menunjukkan lengkungan di atas (OE). Berikut adalah contoh kurva Lorenz ekstrem.
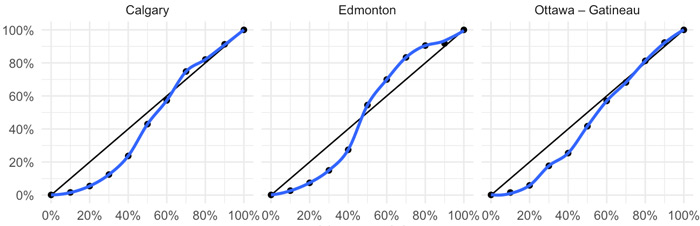
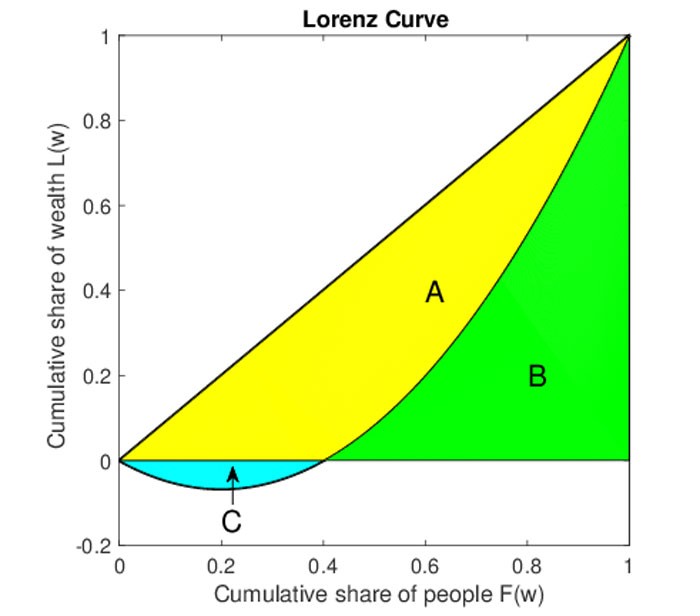
Rumus Kurva Lorenz
Kurva Lorenz termasuk dalam salah satu materi ekonomi yang memiliki rumus paling sedikit. Dimana rumus utamanya hanyalah penghitungan Koefisien Gini serta rumus persentase kontribusi kelompok terhadap total penghasilan.
- Koefisien Gini = A/(A+B)
- Kontribusi Kelompok (%) = Penghasilan Kelompok/Penghasilan Area = (PK)/(PA).
Contoh Soal Kurva Lorenz
Cara termudah untuk mempelajari kurva Lorenz yaitu melalui cara mengerjakan soal. Oleh karena itu, di sini Kursiguru akan membagikan beberapa contoh soal kurva Lorenz beserta jawaban dan pembahasannya. Demi mempersingkat waktu silakan simak langsung contoh persoalan kurva Lorenz berikut ini.
Contoh Soal (1) Kurva Normal
Dalam sebuah lokasi bernama Unknown Area terdapat 100 orang. Setiap individu di Unkown Area memiliki penghasilan dalam rentang 20.000.000 hingga 160.000.000. Jika rincian penghasilan semua orang di Unknown Area tertera seperti dalam tabel (1), gambarlah kurva Lorenz lalu analisa kondisi kemerataan penghasilan di lokasi tersebut.
| Kelompok Masyarakat (KM) | Orang Ke (O) | Penghasilan (P) |
|---|---|---|
| 1 | 1 – 20 | 20.000.0000 |
| 2 | 21 – 40 | 40.000.000 |
| 3 | 41 – 60 | 60.000.000 |
| 4 | 61 – 80 | 120.000.000 |
| 5 | 81- 100 | 160.000.000 |
Jawaban :
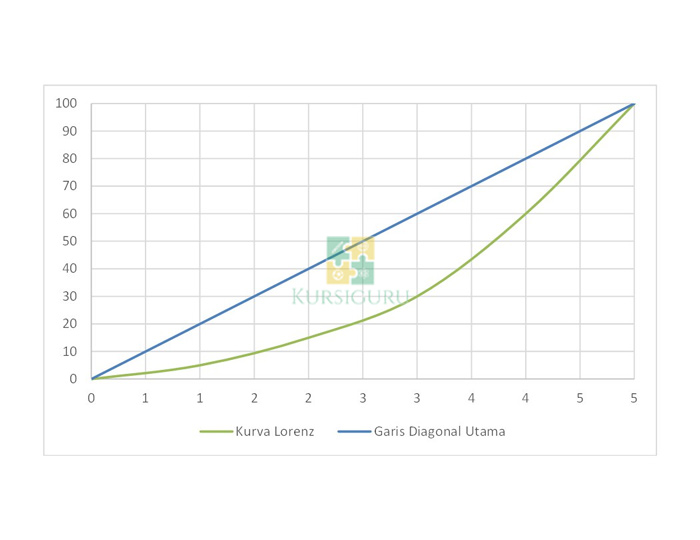
Area A = 0,18
Area B = 0,32
Koefisien Gini = A/(A+B) = 0,18/0,5= 0,36.
Jadi jika melihat pada koefisien Gini nya, maka di lokasi Unknown Area terjadi kemerataan pendapatan.
Contoh Soal (2) Kurva Ekstrem
Berdasarkan contoh soal (1), lakukanlah perhitungan gambarlah kurva Lorenz lalu analisa kondisi kemerataan penghasilan apabila rincian datanya berubah menjadi seperti di bawah ini.
| Kelompok Masyarakat (KM) | Orang Ke (O) | Penghasilan (P) |
|---|---|---|
| 1 | 1 – 20 | – 10.000.0000 |
| 2 | 21 – 40 | – 20.000.000 |
| 3 | 41 – 60 | 60.000.000 |
| 4 | 61 – 80 | 160.000.000 |
| 5 | 81- 100 | 200.000.000 |
Jawaban :
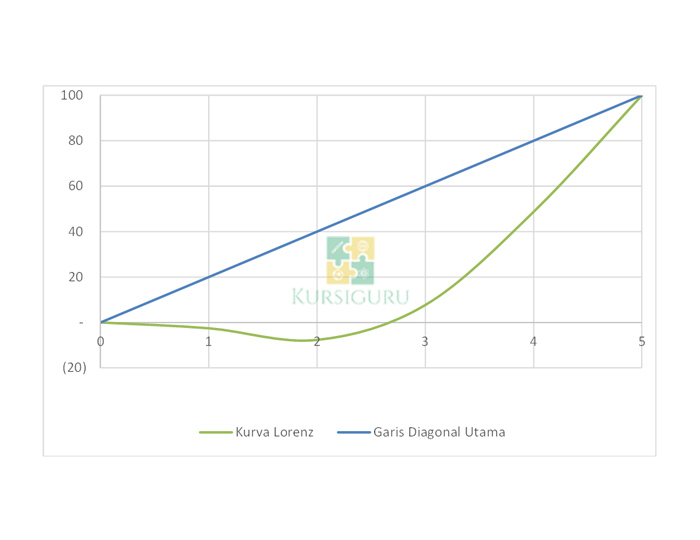
Area A = 0,22
Area B = 0,28
Koefisien Gini = A/(A+B) = 0,19/0,5= 0,44.
Meskipun memiliki koefisien Gini tak berbeda jauh dari contoh soal pertama, namun karena adanya kurva di bawah garis horizontal menjadikan kurva Lorenz soal nomor 2 memiliki kondisi ekstrem. Atau dengan kata lain, pada contoh soal di atas mungkin terjadi pergeseran Nilai Waktu Uang akibat inflasi.
Download Contoh Latihan Soal Kurva Lorenz
Proses pengolahan data kedua soal diatas bisa didownload pada file Excel berikut ini.
Untuk memudahkan proses belajarmu, berikut ini penulis sertakan beberapa contoh persoalan kurva dalam bentuk file PDF. Dimana file contoh soal Lorenz Curve tersebut bisa didownload secara langsung tanpa perlu membayar terlebih dahulu.
Akhir Kata
Demikian pembahasan Kursiguru terkait contoh soal kurva Lorenz beserta jawaban dari setiap soal. Semoga dapat menjadi acuan pembelajaran baik di sekolah ataupun di rumah. Apabila masih memiliki pertanyaan seputar kurva Lorenz, silakan tuliskan di kolom komentar.

Apa jawaban contoh soal kurva lorenz