Contoh Soal Perbandingan adalah jenis soal matematika yang sudah mulai dipelajari sejak di sekolah dasar hingga sekolah menengah atas. Tentunya hal tersebut diiringi dengan tingkat kesulitan soal yang semakin bertambah seiring naiknya jenjang sekolah.
Materi perbandingan pada hakikatnya membandingkan besaran sebuah nilai terhadap satu atau beberapa nilai lainnya. Sebagai contoh paling sederhana adalah kecepatan lari dua orang, jumlah benda milik dua orang, dan sebagainya. Contoh soal seperti itu biasanya diberikan pada siswa sekolah dasar (SD) di kelas 5 ataupun 6.
Semakin naik jenjangnya, tingkat kompleksitas soal-soal perbandingan akan meningkat. Soal untuk siswa SMP tak lagi memberikan perbandingan satu variabel melainkan dua atau lebih variabel. Sedangkan untuk siswa SMA, soal perbandingan tak lagi menjadi pokok bahasan, namun sudah dimasukkan dalam bentuk soal lainnya.
Sebelum lari ke contoh soal, Kursiguru akan mengajakmu memahami terlebih dulu tentang pengertian, sifat, dan rumus materi perbandingan. Dengan memahaminya, proses pengerjaan soal perbandingan akan menjadi mudah. Langsung saja simak penjelasan berikut ini.
Pengertian Perbandingan
Perbandingan merupakan sebuah cara membandingkan antara dua nilai atau lebih dari suatu besaran sejenis, kemudian dinyatakan dengan cara sederhana. Perbandingan dapat ditulis dengan secara matematis yaitu a:b dan bisa ditulis dalam pecahan yaitu a/b.
Contoh penerapan nyata terkait materi perbandingan adalah sebuah peta ataupun globe. Karena tidaklah mungkin seseorang dapat membuat peta dalam sebuah kertas yang ukurannya benar-benar sesuai dengan ukuran bumi. Agar lebih mudah memahami terori perbandingan, simaklah jenis perbandingan beserta contoh soalnya berikut ini.
Contoh Soal Perbandingan Beserta Jawaban & Pembahasannya
Di bawah ini adalah jenis-jenis perbandingan yang muncul dalam materi matematika SD maupun SMP. Uraian terkait jenis perbandingan dari kursiguru juga mencakup contoh soal dan pembahasannya. Oleh karena itu, simaklah pembahasan jenis perbandingan dari kursiguru berikut ini.
1. Perbandingan Pecahan
Perbandingan pecahan merupakan bentuk perbandingan yang melihat dua pecahan dan menentukan besar dari dua pecahan tersebut. Agar dapat menentukan perbandingan dua pecahan, kita harus membuat kedua pecahan tersebut memiliki penyebut sama. Kemudian melihat pecahan mana yang pembilangnya lebih besar.
Contoh Soal:
Antara 20/25, 18/20, dan 24/30 manakah pecahan paling besar besar?
Jawaban:
20/25 diubah menjadi 4/5
18/20 diubah menjadi 4,5/5
24/30 diubah menjadi 4/5
Jadi pecahan 18/20 adalah yang paling besar diantara ketiganya.
Pembahasan:
Meskipun pecahan 24/30 terlihat lebih besar dari pecahan lain, tapi ketika penyebutnya disamakan justru 18/20 lah yang paling besar. Itulah alasan mengapa perbandingan pecahan harus diubah menjadi satu bentuk penyebut lebih dulu.
2. Perbandingan Senilai
Perbandingan senilai merupakan jenis perbandingan bervariabel lebih dari satu. Dimana salah satu nilai variabel diperbesar, dengan begitu nilai variabel lainnya semakin besar.
Contoh Soal:
Jika lele sebanyak 10.000 ekor mampu ditampung oleh kolam berukuran 30 m², berapa ukuran kolam yang dibutuhkan bila jumlah lelenya 20.000 ekor?
Jawaban:
10.000 -> 30 m²
20.000 -> k m²
k = 20.000/10.000 × 30 = 60 m²
Jadi besarnya ukuran kolam lele agar mampu menampung sejumlah 20.000 ekor adalah 60 m².
Pembahasan:
Memperbesar besaran jumlah lele akan memperbesar nilai kolam, itulah artinya makin besar salah satu variabel maka semakin besar pula variabel lainnya.
Contoh Soal Lain:
Misalkan saja Wahyu akan pulang dari kampus ke rumah yang berjarak 10 km, sedangkan bensin di motor Wahyu tersisa 0,5 liter. Jika kemampuan tempuh motor Wahyu adalah 50 km per 2 liter, apakah bensin Wahyu mencukupi untuk sampai rumah?
Jawaban:
2 L = 50 km
0,5 L = z km
z = 0,5/2 × 50 = 12,5 km
Dari perhitungan di atas, maka sisa bensin motor Wahyu masih cukup untuk sampai rumah, karena motornya masih bisa menempuh jarak 12,5 km sedangkan jarak kampus Wahyu dengan rumah hanya 10 km.
Pembahasan:
Contoh soal di atas memberikan gambaran lain dari perbandingan senilai, yaitu saat salah satu nilainya diperkecil maka nilai lain juga makin kecil.
3. Perbandingan Berbalik Nilai
Perbandingan berbalik nilai adalah sebuah perbandingan dengan salah satu nilai variabel diperbesar menjadikan nilai variabel lainnya menjadi kecil. Hal ini bertentangan dengan teori perbandingan senilai di atas. Pada umumnya, soal perbandingan berbalik variabelnya berhubungan dengan waktu.
Soal-soal perbandingan berbalik nilai ini cukup menjebak, karena jika tidak teliti kamu bisa mengerjakannya menjadi perbandingan senilai. Cara agar tidak terjebak adalah memperkirakan jawaban soal melalui logika terlebih dulu.
Contoh Soal:
Pembangunan sebuah rumah memerlukan waktu 1 bulan jika dilakukan oleh 20 orang pekerja. Jika ada penambahan pekerja sebanyak 10 orang, maka berapa lama waktu pembangunan rumah tersebut?
Jawaban:
20 pekerja = 1 bulan (30 hari).
Penambahan 10 pekerja sehingga total pekerja adalah 30 orang.
30 pekerja = v bulan
v = 20/30 × 30 hari = 20 hari
Maka pembangunan rumah menjadi hanya membutuhkan 20 hari atau 2/3 bulan.
Pembahasan:
Dari contoh soal di atas, secara logika sudah bisa dipastikan bahwa semakin banyak pekerjanya makin cepat juga proses pembangunan rumahnya.
Contoh Soal Lain:
Dalam peternakan Farming Mania, 15 ekor sapi mampu menghabiskan rumput di sebuah lapangan dalam waktu 10 hari. Jika pemilik Farming Mania menjual sapinya sebanyak 5 ekor, berapa lama waktu yang dibutuhkan oleh sapi yang tersisa untuk menghabiskan rumput di sebuah lapangan?
Jawaban:
15 sapi = 10 hari
Pengurangan 5 ekor menjadi 10 ekor sapi.
10 sapi = n hari?
n = 15/10 × 10 hari = 15 hari
Maka sisa sapi di peternakan Farming Mania akan membutuhkan waktu selama 15 hari untuk membabat habis rumput di sebuah lapangan.
Pembahasan:
Berkebalikan dari soal pekerja rumah, soal ini memberikan gambaran bahwa semakin sedikit jumlah satu variabel maka nilai lainnya justru makin besar.
4. Perbandingan Selisih
Berbeda dengan perbandingan sebelumnya, perbandingan selisih biasanya digunakan untuk membandingkan umur, jumlah uang, dan tinggi badan.
Contoh:
Ibu Budi baru melahirkan bayi dengan tinggi badan 48 cm. Jika tinggi Budi 72 cm lebih tinggi dari adiknya itu, maka berapa perbandingan tinggi Budi dan adiknya?
Jawaban:
Tinggi adik Budi = 48 cm
Tinggi Budi = 48 + 72 = 120 cm
120:48 = 5:2
Jadi perbandingan tinggi antara adik Budi dan Budi adalah 2:5.
Pembahasan:
Dari contoh soal di atas bisa diketahui bahwa selisih tidak bisa dihitung secara langsung, melainkan besarnya variabel harus dicari secara lengkap terlebih dulu.
Untuk soal perbandingan umur dan penyelesaiannya bisa kamu simak lebih lanjut di dalam artikel perbandingan umur.
5. Perbandingan Trigonometri
Perbandingan trigonometri, sesuai namanya merupakan perbandingan yang bersumber dari bangun datar segitiga. Bentuk soal perbandingan trigonometri paling sering ditemui pada segitiga siku-siku.
Coba perhatikan segitiga ABC siku-siku di bawah ini:
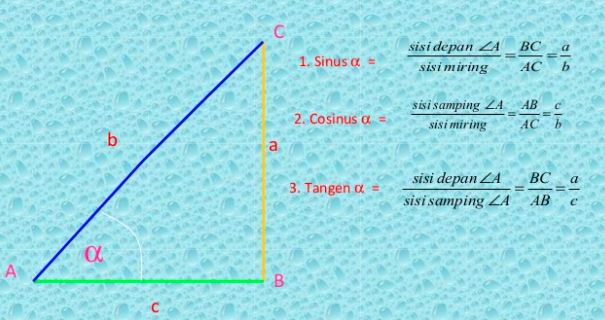
Berdasar gambar di atas, besarnya nilai a, b, serta c saling berhubungan satu sama lain.
Contoh Soal:
Dua buah segitiga siku-siku sebangun masing-masing memiliki besaran sisi tinggi (a) sebesar 6 cm dan 12 cm. Jika pada segitiga pertama sisi miringnya bernilai 10 cm, tentukan perbandingan luas keduanya!
Jawaban:
a1 = 6 cm ; c1 = 10 cm ; a2 = 12, maka:
a2 = b2/b1 × a1
a2 = 12/6 × 10 = 20 cm
Berdasarkan rumus trigonometri, alas tiap segitiga besarnya adalah 8 cm dan 16 cm, sehingga luasnya adalah:
L1 = 1/2 × 6 × 8 = 24 cm2
L2 = 1/2 × 12 × 16 = 96 cm2
Sehingga perbandingan luasan dua segitiga tersebut adalah 24:96 atau 1:4.
Pembahasan:
Perbandingan dalam soal trigonometri di atas merupakan bentuk sederhana. Untuk tingkat lanjut, soalnya akan membandingkan hasil sinus, cosinus, serta tangen nya.
Download Contoh Soal Perbandingan
Setelah kita berkutat pada pembahasan di atas, Kursiguru akan berbagi contoh soal perbandingan untuk tambahan bahan belajarmu. Ada sekitar 48 soal dalam file bawah ini. File di bawah ini berbentuk PDF, sehingga kamu bisa mencetaknya dengan gampang.
Demikian artikel mengenai contoh soal perbandingan yang bisa Kursiguru berikan. Semoga mampu membuatmu paham dengan perbandingan dan cara mengerjakan soalnya. Jangan lupa bagikan artikel ini pada teman-temanmu.
